# 树

树（Tree）是一种由一系列节点组成的具有层次关系的数据结构。

在树中，除了根节点外，每个节点只有一个父节点，每一个节点都有零个或多个子节点，没有子节点的节点称为叶子节点，相邻节点称为兄弟节点，每个节点以及后代构成了一棵子树。

节点的高度是从该节点向下到叶子节点的最大长度，树的高度就是根节点的高度。节点的深度是从该节点向上到根节点的祖先节点数量。节点的层数是该节点的深度加 1。

# 二叉树

二叉树（Binary tree）是一种每个节点最多有两个子节点的树结构。这两个子节点分别是左子节点和右子节点。

# 二叉树的类型

二叉树根据叶子节点的分布可以归纳出两种类型：完全二叉树和满二叉树。

除最后一层外其它层都是满的，如果最后一层的所有叶子节点尽可能的靠左，则是一棵完全二叉树，如果最后一层的叶子节点都存在，则是一棵满二叉树。

# 二叉树的表示

二叉树可以通过基于指针（或引用）的链表和基于下标（或索引）的数组表示。

使用链表表示二叉树时，其中每个节点就是一个对象，对象中包含节点的数据以及指向左右子节点的指针。

class TreeNode {
  constructor(data) {
    this.data = data;
    this.left = left;
    this.right = right;
  }
}

使用数组表示二叉树时，每个节点就是一个数组元素，节点之间的父子关系通过下标计算得到。一般来说，为了计算方便，下标为 1 的位置存储根节点；下标为 2i 的位置存储左子节点；下标为 2i + 1 的位置存储右子节点；以此类推，下标为 i / 2 的位置就是父节点。

使用数组可以有效的表示完全二叉树，因为根据完全二叉树的性质，节点与节点之间是连续的，这样在充分利用数组随机访问特性的同时，又不会浪费太多空间（仅浪费了下标为 0 的数组存储空间）。

# 二叉树的遍历

二叉树的遍历包括前序遍历、中序遍历、后序遍历和层次遍历。这里的前序、中序和后序指的是根节点与左右子树的位置。

# 前序遍历（根-左-右）

前序遍历首先遍历根节点，然后遍历左子树的节点，最后遍历右子树的节点。

function preorderTraversal(root) {
  if (!root) return;
  console.log(root.data);
  preorderTraversal(root.left);
  preorderTraversal(root.right);
}

# 中序遍历（左-根-右）

中序遍历首先遍历左子树的节点，然后遍历根节点，最后遍历右子树的节点。

function inorderTraversal(root) {
  if (!root) return;
  inorderTraversal(root.left);
  console.log(root.data);
  inorderTraversal(root.right);
}

# 后序遍历（左-右-根）

后序遍历首先遍历左子树的节点，然后遍历右子树的节点，最后遍历根节点。

function postorderTraversal(root) {
  if (!root) return;
  postorderTraversal(root.left);
  postorderTraversal(root.right);
  console.log(root.data);
}

# 层次遍历

层次遍历从根节点开始逐层从左到右遍历所有节点。层次遍历基于广度优先搜索和深度优先搜索算法实现。

# 基于广度优先搜索算法实现的层次遍历

以队列辅助结构，首先将根节点入队，然后出队当前节点的并将节点值存储在当前层的数组中，最后依次将当前节点的左右子节点加入到队列中，直到下一层没有节点为止。

function levelorderTraversal(root) {
  if (!root) return [];

  const res = [];
  const queue = [root];
  while (queue.length) {
    const level = [];
    const size = queue.length;
    for (let i = 0; i < size; i++) {
      const node = queue.shift();
      level.push(node.val);
      if (node.left) queue.push(node.left);
      if (node.right) queue.push(node.right);
    }
    res.push(level);
  }
  return res;
}

# 基于深度优先搜索（递归）算法实现的层次遍历

通过递归依次将当前深度的节点的值放入到当前层级数组中，并将当前层级信息传给下一次递归，直到递归完所有节点为止。

function levelorderTraversal(root) {
  if (!root) return [];

  const helper = (node, level) => {
    if (!node) return;
    if (level >= res.length) {
      res.push([]);
    }
    res[level].push(node.val);
    helper(node.left, level + 1);
    helper(node.right, level + 1);
  };

  const res = [];
  helper(root, 0);
  return res;
}

# 基于深度优先搜索（迭代）算法实现的层次遍历

以栈作为辅助结构，首先将根节点和根节点的层级信息入栈，然后出栈当前节点和当前节点的层级信息，并将当前节点的值存储到当前层的数组中，最后从右到左将节点放入栈中，直到遍历完所有节点为止。

function levelorderTraversal(root) {
  if (!root) return [];

  const res = [];
  const stack = [[root, 0]];
  while (stack.length) {
    const [node, level] = stack.pop();
    if (level >= res.length) res[level] = [];
    res[level].push(node.val);
    if (node.right) stack.push([node.right, level + 1]);
    if (node.left) stack.push([node.left, level + 1]);
  }
  return res;
}

以上二叉树遍历的代码时间和空间复杂度都为 O(n)。

# 二叉搜索树

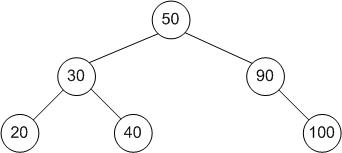
二叉搜索树（Binary search tree，简称 BST），也称二叉查找树或者有序二叉树。二叉搜索树每个节点的值都大于左子树任意节点的值，且小于右子树任意节点的值。根据二叉搜索树有序性的特点，我们可以根据中序遍历，有序的输出所有节点。

二叉搜索树

二叉搜索树的结构，由一个值为 null 的根节点构成。

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
}

# 查找操作

# 指定值

在二叉搜索树中查找指定值的节点。如果指定值的节点存在，返回该节点；否则如果不存在，返回 null。

search(data) {
  return this.searchNode(this.root, data);
}
// 基于递归
searchNode(node, data) {
  if (!node || data === node.data) return node;
  return this.searchNode(data < node.data ? node.left : node.right, data);
}
// 基于迭代
searchNode(node, data) {
  while (node) {
    if (data === node.data) return node;
    node = data < node.data ? node.left : node.right;
  }
  return null;
}

我们首先从根节点开始查找，如果树为空，查找的值不存在，则返回 null；如果查找的值等于根节点的值，则返回该节点；如果查找的值小于根节点的值，则继续在左子树查找；如果查找的值大于根节点的值，则继续在右子树查找。重复这个过程，直到找到指定值的节点或者当前子树为空（也就是该值不存在）为止。

# 最小和最大节点

我们从根节点开始沿着左子节点查找直到当前节点的左子节点为空为止，即可得到最小节点。

min() {
  return this.minNode(this.root);
}
// 基于递归
minNode(node) {
  if (!node) return null;
  if (!node.left) return node;
  return this.minNode(node.left);
}
// 基于迭代
minNode(node) {
  while (node && node.left) {
    node = node.left;
  }
  return node;
}

如果根节点为空，则返回 null；如果根节点的左子节点为空，最小节点就是根节点；如果根节点的左子节点不为空，则最小节点在左子树中，需要继续向左查找。

我们从根节点开始沿着右子节点查找直到当前节点的右子节点为空为止，即可得到最大节点。

max() {
  return this.maxNode(this.root);
}
// 基于递归
maxNode(node) {
  if (!node) return null;
  if (!node.right) return node;
  return this.maxNode(node.right);
}
// 基于迭代
maxNode(node) {
  while (node && node.right) {
    node = node.right;
  }
  return node;
}

# 后继和前驱节点

有时候我们需要按中序遍历的次序查找指定节点的后继节点。后继节点是大于指定节点的最小节点。如果指定节点的后继节点存在，则返回它的后继节点；如果指定节点是树的最大节点，则返回 null。

successor(node) {
  this.successor(this.root, node);
}
successorNode(root, node) {
  if (node.right) this.minNode(node.right);
  let successor = null;
  while (root) {
    if (root.data > node.data) {
      successor = root;
      root = root.left;
    } else {
      root = root.right;
    }
  }
  return successor;
}

查找指定节点后继节点的过程主要包括两种情况。如果指定节点的右子树非空，那么它的后继节点是右子树中的最小节点；如果指定节点的右子树为空，那么它的后继节点是拥有左子节点且是指定节点祖先节点的父节点。

前驱节点与后继节点正好相反，是小于指定节点的最大节点。

predecessor(node) {
  return this.predecessorNode(this.root, node);
}
predecessorNode(root, node) {
  if (node.left) return this.maxNode(node.left);
  let predecessor = null;
  while (root) {
    if (root.data < node.data) {
      predecessor = root;
      root = root.right;
    } else {
      root = root.left;
    }
  }
  return predecessor;
}

# 插入操作

二叉搜索树的插入操作需要从根节点开始向下比较节点并根据结果向左或向右移动节点，直到当前节点移动方向的节点为 null 为止，最后在该方向插入节点。

insert(data) {
  this.root = this.insertNode(this.root, data);
}
// 基于递归
insertNode(node, data) {
  if (!node) return new TreeNode(data);
  if (data < node.data) node.left = this.insertNode(node.left, data);
  else node.right = this.insertNode(node.right, data);
  return node;
}
// 基于迭代
insertNode(node, data) {
  if (!node) return new TreeNode(data);
  let curr = node;
  while (curr) {
    if (data < curr.data) {
      if (!curr.left) {
        curr.left = new TreeNode(data);
        break;
      }
      curr = curr.left;
    } else {
      if (!curr.right) {
        curr.right = new TreeNode(data);
        break;
      }
      curr = curr.right;
    }
  }
  return node;
}

如果树为空，我们将插入节点作为树的根节点；如果插入节点的数据比当前节点的数据小，并且当前节点没有左子节点，那就直接将新节点作为它的左子节点，如果有左子节点则继续在左子树中比较；如果插入节点的数据比当前节点的数据大，并且当前节点没有右子节点，那么就直接将新节点作为作为它的右子节点，如果有右子节点则继续在右子树中比较。

# 删除操作

二叉搜索树的删除节点操作首先从根节点向下查找删除节点，如果没有找到返回 null，如果找到删除节点后需要考虑三种情况。

删除的节点没有子节点，也就是删除的是一个叶子节点。我们直接将该节点置为 null 即可；
删除的节点有一个子节点。我们需要用删除节点的子节点替换删除节点；
删除的节点有两个子节点。我们需要用删除节点的后继节点，也就是删除节点右子树中最小节点替换删除的节点，然后删除后继节点。

delete(data) {
  this.root = this.deleteNode(this.root, data);
}
deleteNode(node, data) {
  if (!node) return null;
  if (data < node.data) {
    node.left = this.deleteNode(node.left, data);
  } else if (data > node.data) {
    node.right = this.deleteNode(node.right, data);
  } else {
    if (!node.left) return node.right;
    if (!node.right) return node.left;
    const minNode = this.minNode(node.right);
    node.data = minNode.data;
    node.right = this.deleteNode(node.right, minNode.data);
  }
  return node;
}

# 性能分析

二叉搜索树的性能与树的高度成正比。对于有 n 个节点的完全二叉树来说，以上二插搜索树操作的最坏情况时间复杂度为 O(logn)。然后，经过频繁操作后，树可能会退化为一条 n 个节点组成的链表，这些操作最坏情况时间复杂度为 O(n)。为了解决二叉搜索树在动态操作后造成的性能退化问题，可以使用红黑树等平衡二叉搜索树来保证这些操作在最坏情况下时间复杂度为 O(logn)。

# 参考

Wikipedia (opens new window)
《算法导论》
《算法》（第4版）
《数据结构与算法之美》
《学习JavaScript数据结构与算法》（第3版）
数据结构基础系列 (opens new window)
算法面试通关 40 讲 (opens new window)
Problems-LeetCode (opens new window)

← 散列表堆 →